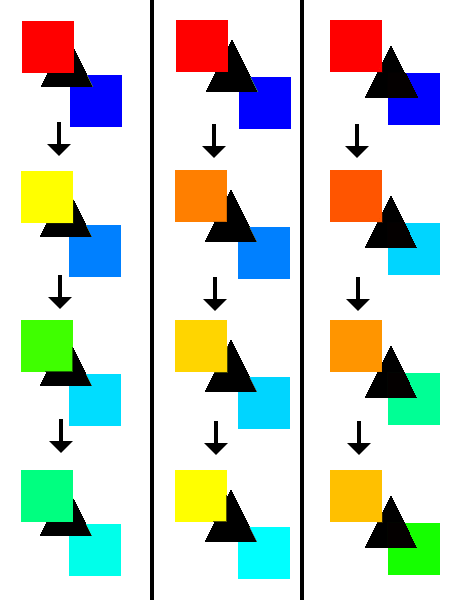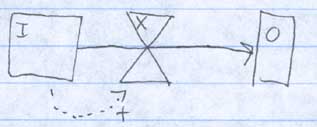
A more complicated model that uses cause and effect arcs requires the use of the triangles to represent rates (as opposed to the implicit constant rates used in the previous example). A triangle pointing upwards represents a rate that has a positive cause-and-effect arc connecting it with its input level. Thus, the flow graph below can be represented by a square overlapping a triangle, overlapping a second square.

The rate constant is now determined by the value of the input level as well as by the percentage of overlap of the shapes. The rate of flow out of the input level is determined by the level of the first square and the percentage of overlap of the first square and the triangle. The rate of flow into of the output level is determined by the level of the first square and the percentage of overlap of the triangle and the second square.

The equations for this model would be:

I = I - (X * the percent overlap)

O = O + (X * the percent overlap)

X = I * C2

where C2 is a global constant.

Because each square can overlap with the triangle in different amounts, the rate of change of the input level may be different than the rate of change of the output value. Column 1 shows a model in which the input level decreases faster than the output value increases. Column 2 shows a situation in which both levels change at approximately the same rate. In column 3, the output increases faster than the input decreases.

back to index

Rules for two squares

Rules for downward pointing triangles

Rules for triangles overlapping with only one square and for multiple overlapping triangles

Note on the image: In the final version the triangle's color will change according to the current rate value.